Graph Measures

A graph measure is a product of an algorithm applied to the graph. These measures reflect meaningful details about the node connectivity as well as its edge characteristics.

Please read below about the graph measures used in uni-layer graphs. We will indicate to which kind of graph a given measure belongs by using W (= weighted graphs) or B (= binary graphs), and D (= directed graphs) or U (= undirected graphs). If no letter is indicated it means that the measure applies to both cases.

Degree
Figure 1: Degree of a node. The red node has a high degree (i.e. a large number of connections), while the blue node has a low degree (i.e. a low number of connections).
Figure 1: Degree of a node. The red node has a high degree (i.e. a large number of connections), while the blue node has a low degree (i.e. a low number of connections).

Degree (nodal): Total number of edges connected to a node.
Average degree (global): Average of the degrees of all nodes.
In-degree (nodal, D): Number of inward edges going into a node.
Average in-degree (global, D): Average of the in-degrees of all nodes.
Out-degree (nodal, D): Number of outward edges originating from a node.
Average out-degree (global, D): Average of the out-degrees of all nodes.
Methodological notes: For BU graphs, the degree is calculated as the sum of the number of connections across the rows or columns of the connectivity matrix. For BD graphs, the in-degree is calculated as sum over columns, while the out-degree is calculated as sum over the rows; the degree is the sum of in-degree and out-degree. For W graphs, the weights of the connections are ignored in the calculations by binarizing the connectivity matrix so that only edges with nonzero weights are considered connected.

Strength
Figure 2: Strength of a node. Despite having less connections, the red node has a higher strength (only one connection with a high strength of 0.9), while the blue node has a lower strength (it has 7 connections, each with strength of only 0.1).
Figure 2: Strength of a node. Despite having less connections, the red node has a higher strength (only one connection with a high strength of 0.9), while the blue node has a lower strength (it has 7 connections, each with strength of only 0.1).

Strength (nodal, W): Sum of the weights of all edges connected to a node.
Average strength (global, W): Average of the strengths of all nodes.
In-strength (nodal, WD): Sum of the weights of inward edges going into a node.
Average in-strength (global, WD): Average of the in-strengths of all nodes.
Out-strength (nodal, WD): Sum of the weights of outward edges originating from a node.
Average out-strength (global, WD): Average of the out-strengths of all nodes.
Methodological notes: For WU graphs, strengths are calculated as sums over either rows or columns of the weighted connectivity matrix. For WD graphs, in-strengths (out-strengths) are calculated as sums over columns (rows), and strengths are calculated as sums of in-strengths and out-strengths.
Barrat, Alain, et al. “The architecture of complex weighted networks.” Proceedings of the National Academy of Sciences of the United States of America 101.11 (2004): 3747-3752.

Eccentricity
Figure 3: Distance between nodes. The distance between the two green nodes is the shortest possible path between them (e.g. the red path). Other (longer) paths between the two nodes can also exist (e.g. the blue path).
Figure 3: Distance between nodes. The distance between the two green nodes is the shortest possible path between them (e.g. the red path). Other (longer) paths between the two nodes can also exist (e.g. the blue path).

Eccentricity (nodal): Maximal distance between a certain node and any other node.[2]
Average eccentricity (global): Average of the eccentricities of all nodes.
In-eccentricity (nodal, D): Maximal incoming distance from all other nodes to a node.
Average in-eccentricity (global, D): Average of the in-eccentricities of all nodes.
Out-eccentricity (nodal, D): Maximal outgoing distance from a node to all other nodes.
Average out-eccentricity (global, D): Average of the out-eccentricities of all nodes.
Radius (global): Minimum eccentricity of all nodes.
Diameter (global): Maximum eccentricity of all nodes.
Methodological notes: The distances (the shortest path lengths) between a node and any other node in the graph can be calculated and stored in a distance matrix. The eccentricity of a node is the maximum of all distances calculated for this node. For D graphs, the in-eccentricity (out-eccentricity) is the maximum along columns
(rows) of the distance matrix and the eccentricity is the larger value of the the in-eccentricity and out-eccentricity. For disconnected nodes, the eccentricity is set to NaN.
Harris, John Michael, Jeffry L. Hirst, and Michael J. Mossinghoff. Combinatorics and graph theory. Vol. 2. New York: Springer, 2008.

Path length
Path length (nodal): Average distance from a node to all other nodes.
Characteristic path length (global): Average of the path lengths of all nodes.
In-path length (nodal, D): Average distance from all other nodes to a particular node.
Average in-path length (global, D): Average of the in-path lengths of all nodes.
Out-path length (nodal, D): Average distance from a particular node to all other nodes.
Average out-path length (global, D): Average of the out-path lengths of all nodes.
Methodological notes: The distance between two nodes is defined as the length of the shortest path between those nodes (figure 3). For B graphs, the length of a path is the number of edges. For W graphs, the length of an edge is a function of its weight; typically, the edge length is inversely proportional to the edge weight because a high weight implies a shorter connection. For D graphs, the path length of a node is the average of its in- and out-path lengths. The shortest path lengths between all pairs of nodes can be found using Dijkstra’s algorithm on W graphs and using breadth-first search on binary graphs.
Distance (binodal): The distance of a graph is the shortest path between all pairs of nodes within a layer of the graph.
Edge Number-Distance (binodal): The edge distance number of a graph is the number of edges in the shortest weighted path between two nodes within a layer.
Rubinov, Mikail, and Olaf Sporns. “Complex network measures of brain connectivity: uses and interpretations.” Neuroimage 52.3 (2010): 1059-1069.
Kepner, Jeremy, and John Gilbert, eds. Graph algorithms in the language of linear algebra. Vol. 22. SIAM, 2011.
Triangles
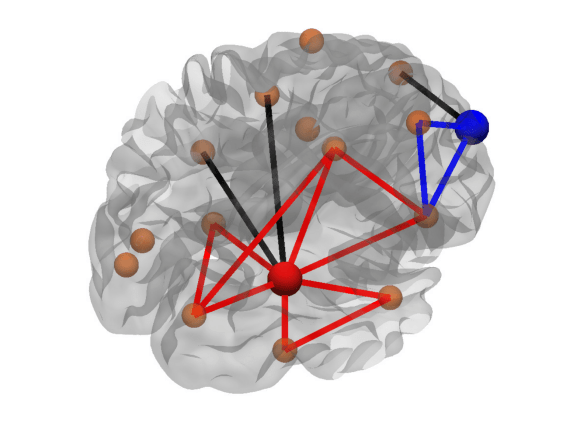
Figure 4: Triangles around a node. The red node has a high number of triangles (only the red edges contribute as the black edges are not connected between themselves), while the blue node has a low number of triangles (only 1 triangle is formed by the blue edges).
Figure 4: Triangles around a node. The red node has a high number of triangles (only the red edges contribute as the black edges are not connected between themselves), while the blue node has a low number of triangles (only 1 triangle is formed by the blue edges).

Triangles (nodal): Number of neighbors of a node that are also neighbors of each other.
Methodological notes: For BU graphs, given a connectivity matrix  A, the number of triangles is the diagonal of A^3 divided by two. For WU graphs, a contribution of the triangles around the node is defined as the geometric mean of the weights of the edges forming the triangle; it can be calculated by taking each element of the connection matrix to the power of 1/3 and the diagonal entries of the third power of the resulting matrix divided by two. For D graphs, we will consider that there is a triangle only if the directed edges between the three nodes (vertices of the triangle) are arranged so that they form a closed cycle (but other conventions are also possible).
Onnela, Jukka-Pekka, et al. “Intensity and coherence of motifs in weighted complex networks.” Physical Review E 71.6 (2005): 065103.

Clustering coefficient
Clustering coefficient (nodal): Fraction of triangles present around a node.
Average Clustering coefficient (global): Average of the clustering coefficients of all nodes.
Methodological notes: The clustering coefficient is calculated as the ratio between the number of triangles present around a node and the maximum number of triangles that could possibly be formed around that node. See also triangles for how the number of triangles is calculated. For U graphs, the total number of possible triangles is calculated as \frac{1}{2}d(d-1), where d is the degree of a node. For D graphs, we consider a triangle only if the directed edges between any three nodes form a cycle; the total number of possible triangles is calculated as d_{\rm in} * d_{\rm out} - d_{\rm ii}, where d_{\rm in} and d_{\rm out} are the in-degree and out-degree of the node, respectively, and d_{\rm ii} is the number of connections that cannot form triangles (i.e. the number of neighboring nodes that are connected with both inward and outward edges).
Watts, Duncan J., and Steven H. Strogatz. “Collective dynamics of ‘small-world’networks.” nature 393.6684 (1998): 440-442.
Transitivity
Transitivity (global): Ratio of total number of triangles to the number of (unordered) triplets in the graph.
Methodological notes: The transitivity is calculated as 3 N_{\rm triangles}/N_{\rm triplets}, where N_{\rm triangles} is the total number of triangles and N_{\rm triplets} is the total number of triplets in the graph. N_{\rm triplets} = \sum_i d_i(d_i-1) - d_{\rm ii}, where the sum runs over all nodes in the graph, d_i is the total degree of each node and d_{\rm ii} are the false pairs that do not result in triplets.
Newman, Mark EJ. “Ego-centered networks and the ripple effect.” Social Networks 25.1 (2003): 83-95.
Closeness centrality
Closeness centrality (nodal): Inverse of the path length of a node.
In-closeness centrality (nodal, D): Inverse of the in-path length of a node.
Out-closeness centrality (nodal, D): Inverse of the out-path length of a node.
Methodological notes: See path length for the calculation of the path length.
Eigen-Vector Centrality (nodal): The eigenvector centrality of a node is the ith element in the eigenvector corresponding to the largest eigenvalue of the graphs adjacency matrix.
Betweenness centrality
Figure 5: Betweeness centrality of a node. The red node has a high betweeness centrality (many shortest paths that connect the nodes from left to right pass through the red node), while the blue node has a low betweeness centrality (no shortest path passes through the blue node).
Figure 5: Betweeness centrality of a node. The red node has a high betweeness centrality (many shortest paths that connect the nodes from left to right pass through the red node), while the blue node has a low betweeness centrality (no shortest path passes through the blue node).

Betweenness centrality (nodal): Fraction of all shortest paths in the graph that pass through a node. Nodes with high values of betweenness centrality participate in a large number of shortest paths.
Edge Betweenness-Centrality (binodal): The edge betweenness centrality of a graph is the fraction of all shortest paths in the graph that pass through a given edge within a layer. Edges with high values of betweenness centrality participate in a large number of shortest paths.
Methodological notes: An algebraic method used to calculate the betweenness centrality is presented by Kintali.
Kintali, Shiva. “Betweenness centrality: Algorithms and lower bounds.” arXiv preprint arXiv:0809.1906 (2008).

Global efficiency
Global efficiency (nodal): Average of the inverse shortest path length from a node to all other nodes.
Average Global efficiency (global): Average of the global efficiencies of all nodes.
In-global efficiency (nodal, D): Average of the inverse shortest in-path lengths of a node.
Average In-global efficiency (global, D): Average of the in-global efficiencies of all nodes.
Out-global efficiency (nodal, D): Average of the inverse shortest out-path lengths of a node.
Average Out-global efficiency (global, D): Average of the out-global efficiencies of all nodes.
Methodological notes: See path length for the calculation of the path length. After the path lengths from a node to all other nodes are calculated, they are inverted and the average gives the global efficiencies of the nodes. For D graphs, the global efficiencies of the nodes are the average of their in- and out-global efficiencies.
Latora, Vito, and Massimo Marchiori. “Efficient behavior of small-world networks.” Physical review letters 87.19 (2001): 198701.
Local efficiency
Local efficiency (nodal): Global efficiency of a node calculated on the subgraph created by the node’s neighbors.
Average Local efficiency (global): Average of the local efficiencies of all nodes.
Methodological notes: See global efficiency for the calculation of the global efficiency. The local efficiency is calculated by applying the same steps on the subgraph formed by the node’s neighbors. In the case of W graph, the weighted connections of the neighbors of node i are calculated as d^{\rm subgraph}_{jk} = d_{jk} \sqrt{d_{ij} d_{ik}}, where the nodes j and k are two neighbors of i, and d_{ij}, d_{ik} and d_{jk} are the weights of the edges.
Modularity
Figure 6: High modularity. This graph is composed by 3 clearly separated communities with a high number of within-module connections and a low number of between-module connections.
Figure 6: High modularity. This graph is composed by 3 clearly separated communities with a high number of within-module connections and a low number of between-module connections.
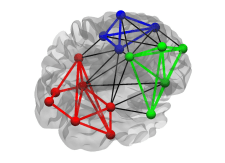
Figure 7: Low modularity. This graphs is the one shown in Figure ref{fig:measures:modularity_high} with some extra between-module connections. The graph can no longer be clearly separated into a collection of communities.
Figure 7: Low modularity. This graphs is the one shown in Figure 6 with some extra between-module connections. The graph can no longer be clearly separated into a collection of communities.

 

 

 

 

 

 

Modularity (global): Extent to which a graph can be divided into clearly separated communities (i.e. subgraphs or modules). Its calculation requires a previously determined community structure.Methodological notes: The modularity is calculated as
\frac{1}{l}\sum_{ij} \left[ A_{ij} -\frac{k_i k_j}{l} \right] \delta_{ij}
where l is the number of edges in the graph, A_{ij} represents the connectivity matrix, k_i (k_j) is the degree of the node i (j), and \delta_{ij} is 1 if the two nodes belong to the same community and 0 otherwise, while the sum is performed over all pairs of nodes in the graph.

Within-module z-score
Figure 8: Within-module z-score of a node. A node can have low z-score because it has a low number of connections (leftmost yellow node) or because it has a lot of connections outside of the community to which it belongs (rightmost yellow node). Nodes with lots of connections within their community have high z-score (e.g. violet node).
Figure 8: Within-module z-score of a node. A node can have low z-score because it has a low number of connections (leftmost yellow node) or because it has a lot of connections outside of the community to which it belongs (rightmost yellow node). Nodes with lots of connections within their community have high z-score (e.g. violet node).

Within-module z-score (nodal): Extent to which a node is connected to the other nodes in the same community. It is a within-module version of degree. Its calculation requires a previously determined community structure.
Within-module in-z-score (nodal, D): Z-score calculated only by considering the contribution of in-path lengths.
Within-module out-z-score (nodal, D): Z-score calculated only by considering the contribution of out-path lengths.
Methodological notes: The z-Score is calculated as
Z_i = \frac{K_i - K_{S_i}}{\sigma_{S_i}}
where K_i is the degree of the node in the community S_i to which the node belongs, K_{S_i} is the average degree of all nodes in the community S_i, and \sigma_{S_i} is the standard deviation of the degree of the nodes within the community S_{i}.

Participation coefficient
Figure 9: Participation coefficient of a node. A node has low participation coefficient if most of its connections are within its community (violet node). It has high participation coefficient if a lot of its connections are with nodes in different communities (yellow node).
Figure 9: Participation coefficient of a node. A node has low participation coefficient if most of its connections are within its community (violet node). It has high participation coefficient if a lot of its connections are with nodes in different communities (yellow node).

Participation coefficient (nodal): Quantifies the relation between the number of edges connecting a node outside its community and its total number of edges. Its calculation requires a previously determined community structure.
Methodological notes: The participation coefficient can be calculated as
P_i = 1 - \sum_s \left( \frac{K_{S_i}}{K_i} \right)^2
where the sum runs over all communities, K_{S_i} is the number of edges connecting the node i within its community S_i, and K_i is the total number of edges of node i. Nodes with a high participation coefficient (known as connector hubs) are connected to many communities and are likely to facilitate global intermodular integration.

Assortativity and Core Structure
Assortativity coefficient (global): The assortativity coefficient is a correlation coefficient between the degrees/strengths of all nodes on two opposite ends of an edge.
Core-periphery (nodal): The core-periphery of a node is the value of the rank corresponding to the maximum richness of nodes. It returns 1 for a node belonging to the core and zero otherwise.
In-In-Assortativity (global): The in-in-assortativity coefficient of a graph is the correlation coefficient between the degrees/strengths of all nodes on two opposite ends of an edge within a layer.  The corresponding coefficient for directed and weighted networks is calculated by using the weighted and directed variants of in-degree/in-strength.
In-Out Assortativity (global): The in-out-assortativity coefficient of a graph is the correlation coefficient between the degrees/strengths of all nodes on two opposite ends of an edge within a layer. The corresponding coefficient for directed and weighted networks is calculated by using the weighted and directed variants of in-out-degree/in-out-strength.
Out-In Assortativity (global): The out-in-assortativity coefficient of a graph is the correlation coefficient between the degrees/strengths of all nodes on two opposite ends of an edge within a layer. The corresponding coefficient for directed and weighted networks is calculated by using the weighted and directed variants of in-out-degree/in-out-strength.
Out-Out Assortativity (global): The out-out-assortativity coefficient of a graph is the correlation coefficient between the degrees/strengths of all nodes on two opposite ends of an edge within a layer. The corresponding coefficient for directed and weighted networks is calculated by using the weighted and directed variants of out-degree/out-strength.
K-Core (binodal): The k-core of a graph is the largest subnetwork comprising nodes of degree k or higher. k is set by the user; the default value is equal to 1.
K-Core Centrality (nodal): The k-coreness centrality of a node is k if the node belongs to the k-core but not to the (k+1)-core.
Rich-Club (global): The rich-club of a node at level k is the fraction of the
edges that connect nodes of degree k or higher out of the maximum number of edges that such nodes might share within a layer. k is set by the user, the default value is equal to 1.
Rich-Club Degree (nodal): The rich-club degree of a node at level k is the sum of
the edges that connect nodes of degree k or higher within a layer. k is set by the user; the default value is equal to 1.
Rich-Club Strength (nodal): The rich-club strength of a node at level s is the sum of the weighted edges that connect nodes of strength s or higher within a layer.
s is set by the user and it can be a vector containing all the strength thresholds
the default value is equal to 1.
Richness (nodal): The richness of a node is the sum of the edges that connect nodes of a higher degree within a layer.
S-Score (binodal): The s-core of a graph is the largest subnetwork comprising nodes of strength s or higher. s is set by the user; the default value is equal to 1.
Weighted Rich-Club (global): The weighted rich-club of a node at level s is the fraction of the weights of the edges that connect nodes of strength s or higher out of the maximum number of edges weights that such nodes might share within a layer. s is set by the user and it can be a vector containing all the strength thresholds; the default value is equal to 1.
Methodological notes: The assortativity is calculated as
r = \frac{l^{-1}\sum_{i,j\in L }k_i k_j - [l^{-1} \sum_{i,j\in L} \frac{1}{2}(k_i + k_j)]^2}{l^{-1} \sum_{i,j\in L} \frac{1}{2}(k_i^2 + k_j^2) - [l^{-1} \sum_{i,j\in L} \frac{1}{2}(k_i + k_j)]^2}
where k_i and k_j are the respective degrees of the nodes i and j, and l is the number of edges in the graph. The corresponding coefficient for directed and weighted networks is calculated by using the weighted and directed variants of degree/strength. A positive assortativity coefficient indicates that nodes tend to link to other nodes with similar degree/strength.
Newman, M. E. J. “Assortative mixing in networks, 2002.” Phys. Rev. Lett 89: 208701.
Small-worldness
Small-worldness (global): A small-world graph has a similar characteristic path length as a random graph with the same degree distribution but is significantly more clustered.
Methodological notes: The small-worldness coefficient is calculated as
C_{\rm sw} = \frac{C/C_{\rm rnd}}{L/L_{\rm rnd}}
where C and L are the clustering coefficient and characteristic path length of the graph, and C_{\rm rnd} and L_{\rm rnd} are the corresponding expected measures calculated on random graphs (typically averaging more than 100 random graphs). If C_{\rm sw} \gg 1, then the network has a small-world organization.
Watts, Duncan J., and Steven H. Strogatz. “Collective dynamics of ‘small-world’networks.” nature 393.6684 (1998): 440-442.
Humphries, Mark D., and Kevin Gurney. “Network ‘small-world-ness’: a quantitative method for determining canonical network equivalence.” PloS one 3.4 (2008): e0002051.
Community Structure
Community Structure (nodal): The community structure of a graph is a subdivision of the network into non-overlapping groups of nodes which maximizes the number of within-group edges, and minimizes the number of between-group edges.